1.1质点运动的描述
1.1.1参照系 坐标系 质点
运动是物体存在的形式,是物质的固有属性,这称为运动的绝对性。
以不同物体作为参照对同一物体运动的不同描述,称为运动描述的相对性。
研究物体运动时被选择作参照物的物体,称为参照物。
任何物体都是有一定大小、形状。当物体转动或物体有形变时,物体的大小和形状对运动的影响都是重要的.但在有些问题中,这种影响可以忽略,可以把物体当做质点来处理。
1.1.2 位置矢量 位移
在直角坐标系中,确定运动质点P在任意时刻t所在的位置,用x,y,z来表示,当质点的位置随之变化时,x,y,z都是时间t的函数,即x=x(t),y=y(t),z=z(t).①
当然也可以用从O到P点的有向线段OP来表示。OP成为质点的位置矢量(位矢),又称为矢径,常用r表示,如图1-2,r=r(t)= x(t)i+y(t)j+z(t)k②
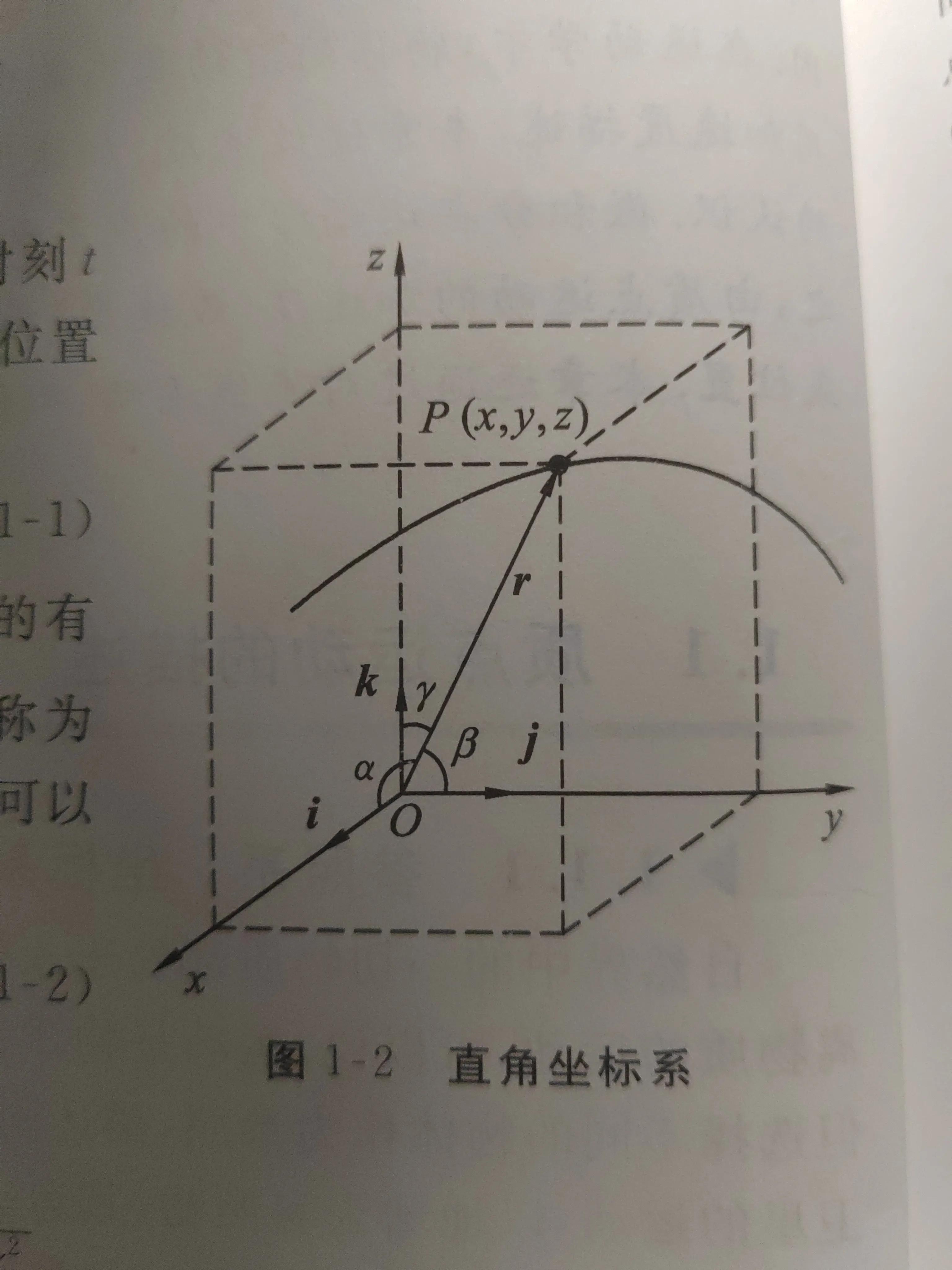
其中,i,j,k是坐标轴x,y,z的单位矢量。位矢r的大小r=|r|=根号x^2+y^2+z^2.表示质点离离坐标原点的距离,而位矢r的方向可以用其余弦方向表示,即cosα=x/y,cosβ=y/r,cosγ=z/r.
①和②称为质点的运动方程.根据问题的条件,求质点的运动方程是力学的基本任务之一。质点在空间运动过程中所经历的路径称为轨道。从①中消去时间t,就可以得到质点的轨道方程,所以①也称为轨道的参数方程。
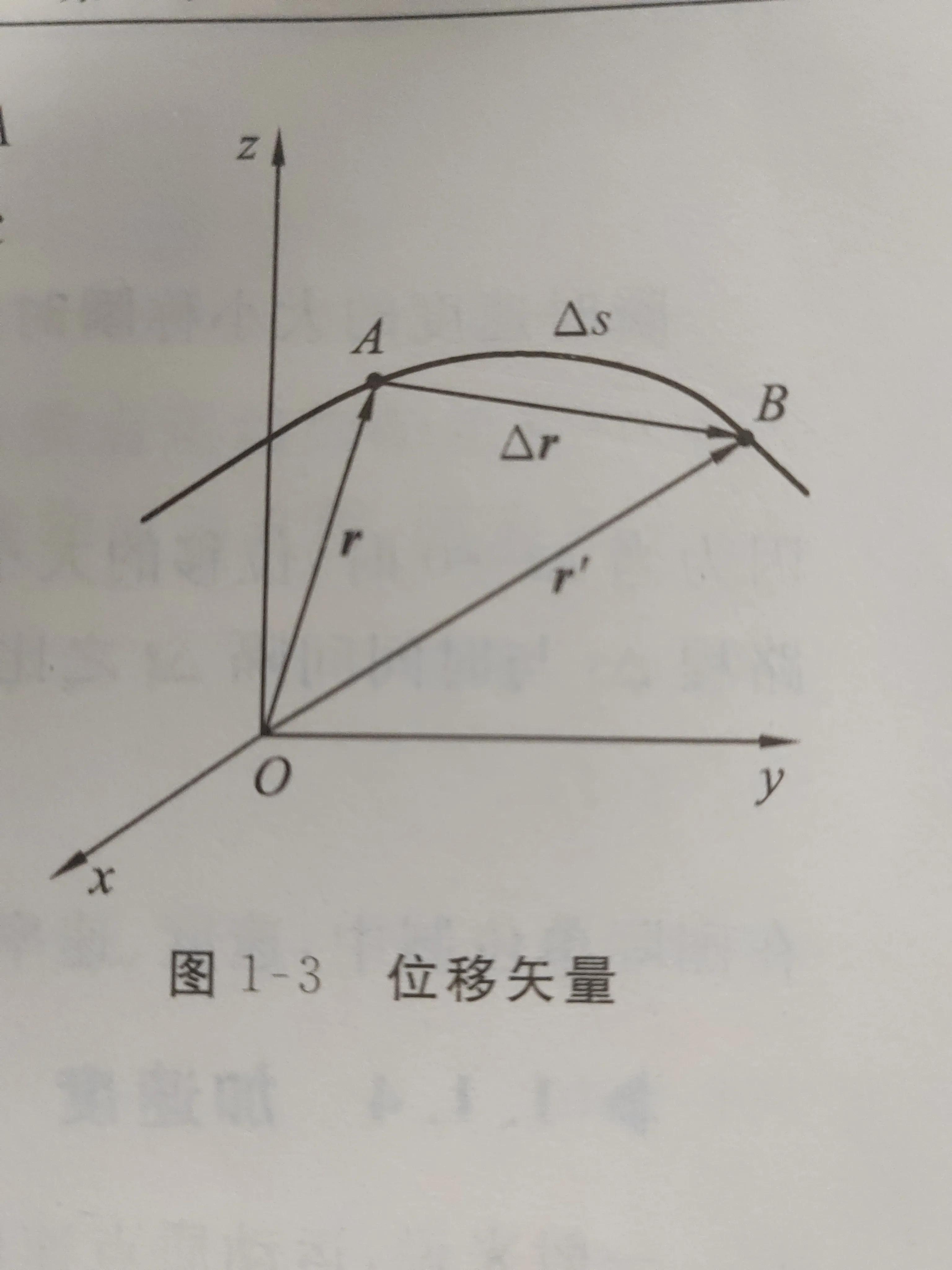
设质点沿某轨道运动,在时刻t,质点的位置在轨道的A处,在时刻t+△t,它在轨道的B处(图1-3).质点在A、B两处的位置矢量分别为r和r’.在时间间隔△t内,质点位置发生了变化,质点位置的变化可以用有向线段AB来表示.从图中可以看出,有向线段AB.就是矢量r的增量△r,即△r=r’-r
△r称为运动质点在时间间隔△t内的位移.位移也是矢量,其方向表明了B点相对于A点的方位,位移的数值|△r|表明了B点与A点之间的直线距离。在△t时间内质点沿轨道(如图所示的曲线)从A点运动到B点,它经过的路径长度,即这一段曲线长度称为路程,用△s表示.
应当注意的是,路程△s和位移△r是两个完全不同的概念,首先,路程△s是标量,位移△r是矢量;其次,路程的长度△s和位移的大小|△r|一般并不相等,只有在时间△r趋近于零时,才可以把△s和|△r|看作相等.
在国际单位制中,位置矢量、位移和路程的常用单位是米(m).
